To size a pump, you must define:
- The flow rate of liquid the pump is required to deliver
- The total differential head the pump must generate to deliver the required flow rate
This is the case for all types of pumps: centrifugal or positive displacement.
Other key considerations for pump sizing are the net positive suction head available (NPSHa) and the power required to drive the pump.
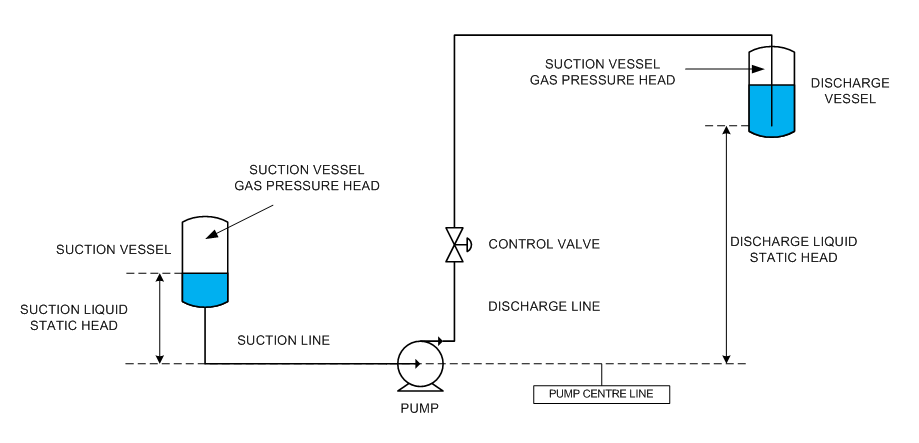
Pump System Diagram
Flow Rate
Usually, the flow rate of liquid a pump needs to deliver is determined by the process in which the pump is installed. This ultimately is defined by the mass and energy balance of the process.
For instance the required flow rate of a pump feeding oil into a refinery distillation column will be determined by how much product the column is required to produce. Another example is the flow rate of a cooling water pump circulating water through a heat exchanger is defined by the amount of heat transfer required.
Total Differential Head
The total differential head a pump must generate is determined by the flow rate of liquid being pumped and the system through which the liquid flows.
Essentially, the total differential head is made up of 2 components. The first is the static head across the pump and the second is the frictional head loss through the suction and discharge piping systems.
Total differential head = static head difference + frictional head losses
Static Head Difference
The static head difference across the pump is the difference in head between the discharge static head and the suction static head.
Static head difference = discharge static head – suction static head
Discharge Static Head
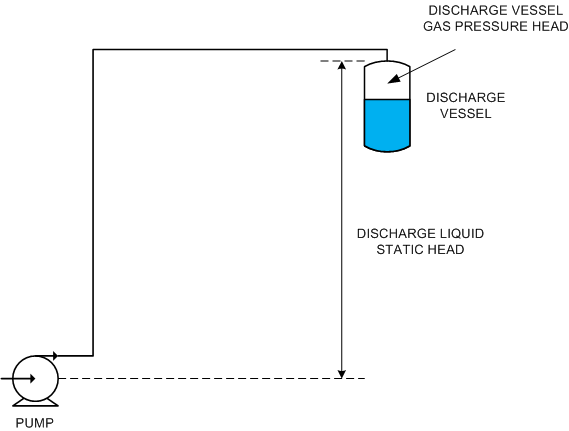
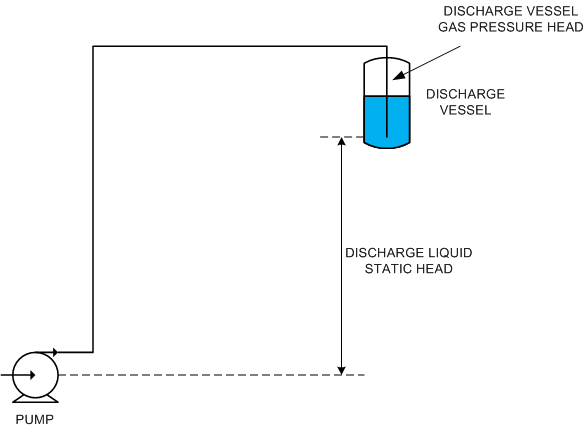
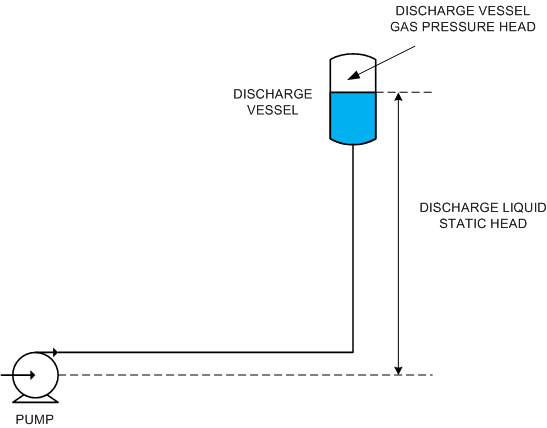
The discharge static head is sum of the gas pressure at the surface of the liquid in the discharge vessel (expressed as head rather than pressure) and the difference in elevation between the outlet of the discharge pipe, and the centre line of the pump.
Discharge static head = Discharge vessel gas pressure head + elevation of discharge pipe outlet – elevation of pump centre line
The discharge pipe outlet may be above the surface of the liquid in the discharge vessel or it may be submerged as shown in these 3 diagrams.
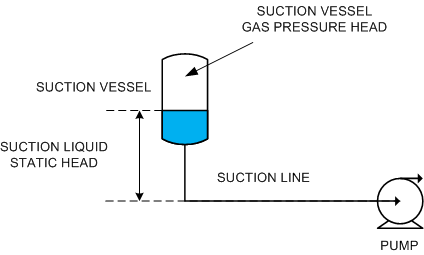
Suction Static Head
The suction static head is sum of the gas pressure at the surface of the liquid in the suction vessel (expressed as head rather than pressure) and the difference in elevation between the surface of the liquid in the suction vessel and the centre line of the pump.
Suction static head = Suction vessel gas pressure head + elevation of suction vessel liquid surface – elevation of pump centre line
Note: gas pressure can be converted to head using: Gas head = gas pressure ÷ (liquid density x acceleration due to gravity)
Frictional Head Losses
The total frictional head losses in a system are comprised of the frictional losses in the suction piping system and the frictional losses in the discharge piping system.
Frictional head losses = frictional losses in suction piping system + frictional losses in discharge piping system
The frictional losses in the suction and discharge piping systems are the sum of the frictional losses due to the liquid flowing through the pipes, fittings and equipment. The frictional head losses are usually calculated from the Darcy-Weisbach equation using friction factors and fittings factors to calculate the pressure loss in pipes and fittings.
Darcy-Weisbach equation:
Where:
\( f =\) pipe friction factor
\( L =\) pipe length
\( D =\) pipe diameter
\( K_{fittings} =\) fittings factor
\( u =\) liquid velocity
\( g =\) acceleration due to gravity
In order to calculate the frictional head losses you therefore need to know the lengths and diameters of the piping in the system and the number and type of fittings such as bends, valves and other equipment.
Net Positive Suction Head Available
The net positive suction head available (NPSHa) is the difference between the absolute pressure at the pump suction and the vapour pressure of the pumped liquid at the pumping temperature.
It is important because for the pump to operate properly, the pressure at the pump suction must exceed the vapour pressure for the pumped fluid to remain liquid in the pump. If the vapour pressure exceeds the pressure at the pump suction, vapour bubbles will form in the liquid. This is known as cavitation and leads to a loss of pump efficiency and can result in significant pump damage.
To ensure that the pump operates correctly the net positive suction head available (NPSHa) must exceed the net positive suction head required (NPSHr) for that particular pump. The NPSHr is given by the pump manufacturer and is often shown on the pump curve.
Net positive suction head available = absolute pressure head at the pump suction – liquid vapour pressure head
Pump Power
Pumps are usually driven by electric motors, diesel engines or steam turbines. Determining the power required is essential to sizing the pump driver.
Pump power = flow rate x total differential head x liquid density x acceleration due to gravity ÷ pump efficiency
How To Size A Pump Example
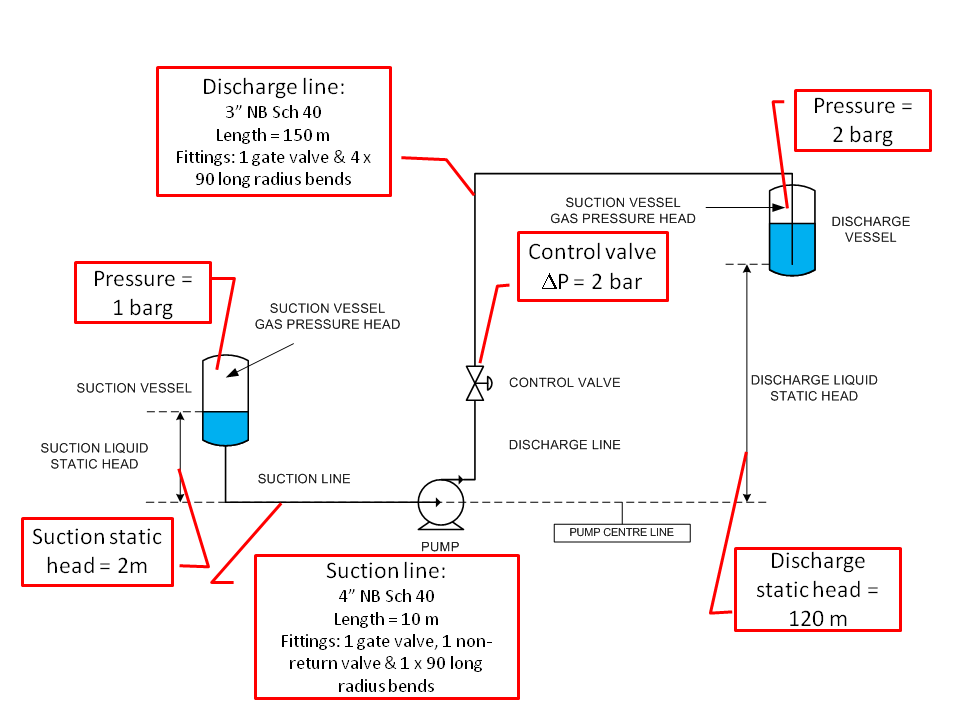
Let’s look at an example to demonstrate how to size a pump.
30000 kg/hr of water needs to be pumped from one vessel to another through the system shown in the diagram below. The water is at 20C, has a density of 998 kg/m3 , a vapour pressure of 0.023 bara and a viscosity of 1cP. We’ll assume that the pump efficiency is 70%.
Calculation
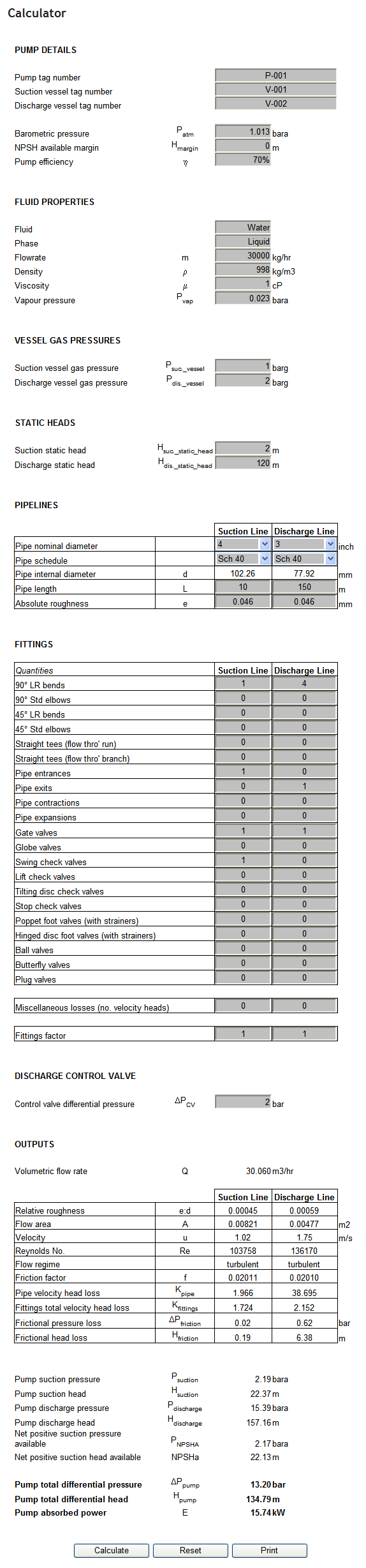
The calculation is presented below:
Results
Pump flow rate = 30 m3/hr
Pump total differential head = 134.8 m
Net positive suction head available = 22.13 m
Pump power = 15.7 kW